低速气动马达定子内表面曲线的生成及优化

　气动马达在石油、矿山、化工、食品及轻纺等行业有广泛运用。现有的气动马达一般是高速小扭矩型的, 而实际中往往需要低速大扭矩型的气动马达。

　　1 .曲线的生成

　　气动马达定子内表面曲线的最小和半径由气动马达的功率参数、结构尺寸及相应约束条件确定。这里主要讨论由最小半径到半径曲线的过渡方式及其对气动马达性能影响的优化问题。

　　参照低速大扭矩液压马达结构 , 根据由曲线构成的径向运动规律, 可将曲线分成为等加速一等减速、有等速过渡区的等加等减速、加速度按正弦规律变化、匀变加速度修正的等加速等类型。为了便于从更广泛的曲线类型中优选出理想的结果, 笔者综合以上各类曲线的特点, 提出两类新的曲线。

　　l) 高次曲线

　　高次曲线的运动方程为

　　边界条件分别由曲线的起始位置、起始速度、起始加速度、终止位置、终止速度、终止加速度确定, 调整a ~ f 参数值得到各种形状的曲线。

　　2 ) 样条曲线

　　利用数值计算方法, 按照柱塞运动规律要求, 设定几个初始点, 对其进行分段的三次

　　H er m it e 插值, 可建立一致连续且光滑的柱塞位移运动规律曲线。

　　2 .确定优化目标函数

　　定子内表面曲线主要影响气动马达瞬态输出扭矩。为提高低速大扭矩气动马达的性能, 这里将气动马达输出平均扭矩大、扭矩脉冲小作为目标函数。

　　由加权组合法可得单目标函数

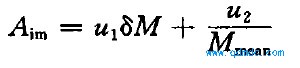
　　式中, 占M 为瞬态扭矩均方根; M ean为瞬态扭矩平均值; u1 和u2: 分别为加权系数, 为突出大扭矩指标, 考虑平均扭矩倒数关系, 这里取U1=1 , U2=2.

　　3 优化方法

　　以定子内表面曲线形状为设计函数, 使目标函数iA m 值最小, 利用单纯形法进行优化设计。

　　具体计算方法是先根据压力特性、流量特性及定子内表面曲线形状, 利用四阶R u n ge Kutta 法, 在计算机上解联立微分方程组, 便可求得柱塞腔的瞬态压力值; 再利用扭矩计算公式即可求出气动马达各时刻的瞬态输出扭矩, 从而得到目标函数Aim 值。对于不同的定子内表面曲线会有不同的浅Aim 值。

　　4 .优化结果的理论比较

　　已知气源压力P=0.7 M P a , 气动马达柱塞直径d ~ 30 m m , 定子内表面最小和最矢

　　径分别86 和10 0 m m , 定子内曲线作用次数为4 , 气动马达柱塞数为6, 膨胀率C=0.28。理论可算出按常规方法设计和优化设计的一种等加一等减速定子内表面曲线的气动马达单个柱塞产生的扭矩材。及整个气动马达瞬态输出扭矩材Mn.( 表1 )

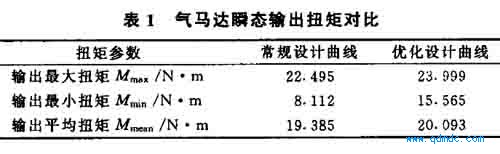
　　由表1 可见, 优化后的气动马达输出平均扭矩略有增大, 而低扭矩有明显增加, 使扭

　　矩脉动降低, 能提高气动马达的整机性能.