气动马达模型的辩识和分析
2017-09-12 来自: 浙江新汕自控阀门有限公司 浏览次数:960
气动马达的防爆性使得它非常适应于化学工业、石油工业等易燃易爆的环境中。虽然目前已有各种防爆式电动机,但用本质安全防爆的标准衡量,它们仍然代替不了气动马达。因此,在现代大规模生产中,气动马达也同其它气动元件一样,被广泛应用在各个控制系统中,并且随着技术发展,对其输出运动的各项指标提出了更高的要求。
但是由于空气的可压缩性,使得气动马达也同其它气动元件一样,在理论建模中具有较大的不确定性,给工程应用带来了很大的不便。因此对气动马达的模型进行辩识十分必要。
1.试验装置的构成
试验装置如图1所示
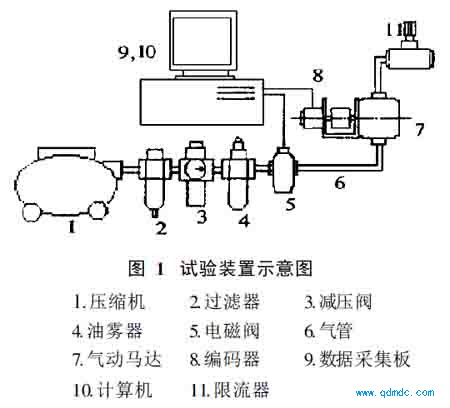
由于气动元件的动力是压缩空气,而压缩空气的水平变化影响到气动元件的动特性,因此,在试验中分三个水平输入压缩空气,即: 0. 6MPa, 0. 4M Pa,0. 2M Pa,每个水平做两组。采样时,将输入信号u和输出信号y 分别纪录,做成数据文件,在采样后,再对数据文件进行各种处理。
在数据处理中,使用的是M ATLAB语言(控制系统计算机辅助设计语言)中系统识别工具箱的各种手段。由于MATLAB语言数据处理和绘图的强大功能,一方面使数据处理大大简化,另一方面,又保证了数据处理的可靠性。
辩识nk 时,先设一个时延范围,然后求其最 佳值;当选定值处于界点时,应重新设量更大范围,直到选定值处于界内。最 佳值是通过最小损失函数自动判定。
时延常数nk 选定后,可在任意阶范围内优选出最 佳阶次。各阶次的最小损失函数分布可通过自动作图看出。
4)在完成模型的辩识后,即可根据此模型进行参数估计。
5)在模型辩识时,除了可以使用最小二乘法外,还可以用M ATLAB系统识别工具箱中的辅助变量法、频谱分析法等算法进行比较。此外,在辩识程序中,除了用残差分析确定的模型外,还多次用由Z1子集得出的模型进行频域和时域的仿真,与参考子集Z2比较(相互确认法) ,以保证模型的正确性。
2.辩别结果及分析
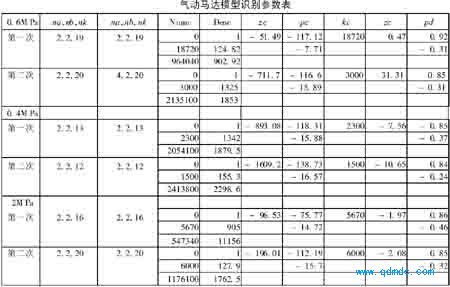
六个试验的数据如下表所示。表中na、nb、nk 分别为上述离散模型的阶次, nk 为延迟时间, numc和denc是连续系统传递函数G( s)分子和分母多项式按拉氏算子S降阶排列的系数; z c、pc、kc 分别是连续系统零、极、增益模型中的零点、极点和增益; z d、pd分别是离散系统G( Z)零、极、增益模型中的零点和极点。分析结果:
1)表中数据表明: 尽管供气压力不同,除一次识别为四阶外,其余均为二阶。由每个模型做出的仿真与参考集Z2具有良好的一致性。因此可以认为: 气动马达模型的阶次是二阶。
2)在这里也应看到: 在三个不同水平的供气压力条件下得到的模型,虽然阶次是二阶,并且各极点一致性较好,但有的零点和增益相差较大,这其中有算法和采样系统误差,但主要是气动系统工作介质的影响。这些参数的离散性,要求相应的控制系统具
有较强的鲁棒性。
3)由控制理论可知: 一个控制系统的全性质都取决于其闭环系统传递函数,而由开环传递函数研究闭环传递函数时,唯有闭环传递函数的极点计算起来比较困难。因此工程上常采用频率响应法和根轨迹法等间接研究方法,分析闭环系统的性质。
NYQUIS T稳定判据是根据开环传递函数的NYQUIS T曲线判断闭环系统是否稳定: 当开环传递函数在右半S 复平面没有极点时, 如果NYQUIS T曲线不包围临界点( - 1+ j0) ,则系统稳定。
从表中可以看出: 不同水平下的开环极点pc 均小于零,即位于S 复平面左边,满足线性控制系统稳定的充要条件。而图4表明: NYQUIS T曲线不包围临界点( - 1+ j0) ,所以当对气动马达施以闭环单位反馈控制时,系统是稳定的。
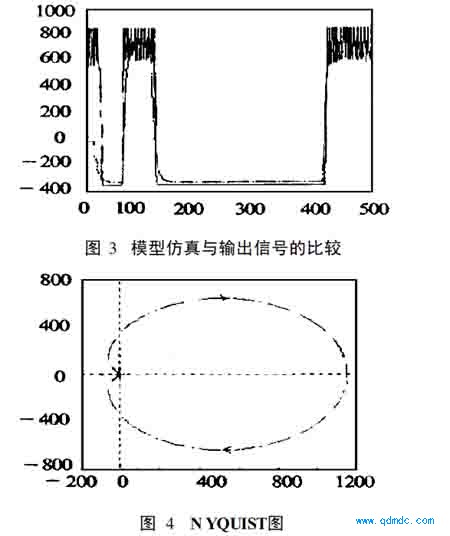
4)根轨迹法是根据开环传递函数的零点和极点的分布,用作图的方法求出闭环极点的分布,是设计和校正控制系统的一种简便方法。图5是气动马达开环传递函数的根轨迹图。
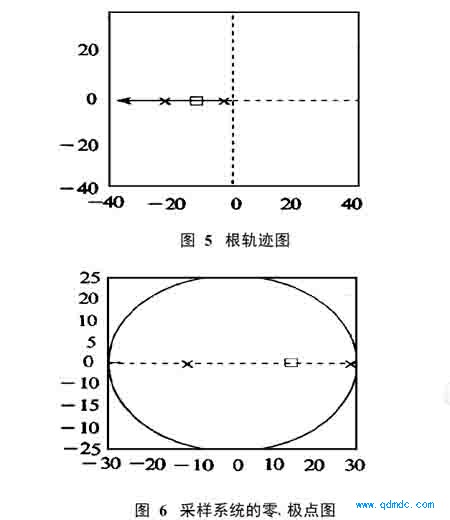
5)图6是根据Z传递函数G( z )作的零极点图。从图中可以看到模型极点pd 的绝 对值均小于1,即在单位圆内,说明该采样系统开环稳定。
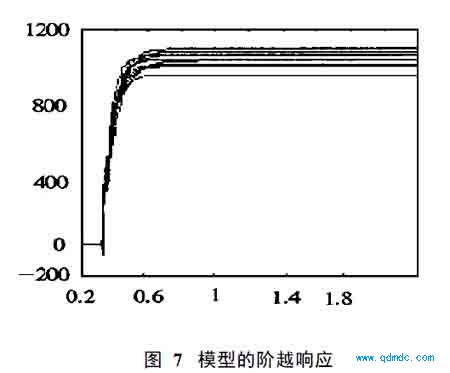
图3到图7是在0. 6Mpa 下做出的。图3是已知模型的仿真与参考集Z2的比较;图7是已知模型的十次阶越响应,包容了模型的误差。
还需要指出的是: 活塞式气动马达本身的结构使得其输出运动具有脉动, 因而, 模型残数( residua l)的主要成份来源于此。
本研究通过试验对气动马达的数学模型进行了辩识,其模型又通过仿真得到验证。用此模型可以对理论模型进行修正。由于在试验中使用了M ATLAB语言,因而使试验工作量大大减少。这种方法可以广泛地应用到对气动元件和气动系统模型的识
别中去,从而推动气动技术在更高层次上的更广泛应用。



