贯穿叶片式气动马达主要参数设计计算
2017-12-13 来自: 浙江新汕自控阀门有限公司 浏览次数:1296
贯穿叶片式气动马达主要参数设计计算
摘要:介绍了贯穿叶片式气动马达的组成部分、工作原理、气缸内壁型线,计算、了解气腔面积、气腔容积及该种马达的主要参数。
关键词:贯穿叶片;气动马达;气腔型线;设计计算
1 概述
贯穿叶片式气动马达可以认为是从贯穿叶片式压缩机或一般叶片式气动马达演变来的,前者与后二者在结构和设计计算的某些方面有若干共同点,但前者比一般叶片式气动马达要简单些。由于一般叶片式气动马达的叶片靠离心力及叶片根部的压缩气体的压力作用使叶片顶部紧紧压向气缸内壁面来实现相邻气腔间的密封,这样,叶片与气缸内壁面之间的摩擦力较大,从而缩短了气动马达叶片寿命,降低了气动马达总效率。
为了克服一般叶片式气动马达的这一缺点,出现了贯穿叶片式气动马达。
2 贯穿叶片式气动马达组成部分
图1为贯穿叶片式气动马达组成部分示意图。该气动马达由转动部分及固定部分组成。转动部分包括图1所示的转子2,转子2上有两条相互垂直的贯穿叶片槽,两槽内装有两个相互垂直的彼此互不干扰的叶片
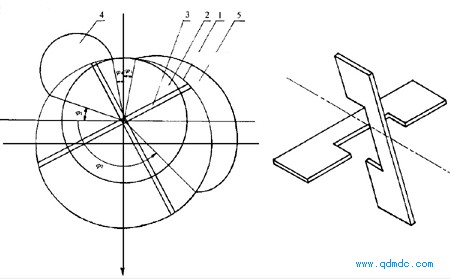
3气动马达运转过程中,叶片顶部始终保持与气缸1的内壁表面接触以防止叶片两侧的气体窜流;但对气缸内壁表面产生很小的接触力。转子2始终绕其中心转动,气动马达输出轴与转子2固结在一起,输出轴的中心线与转子中心线重合(输出轴在图1中未表示出)。
固定部分主要包括图1的气缸1,气缸1的外表面上有进气孔口4及排气孔口5,此二者分别与进气接管及排气接管连通,此二接管图1中未表示出来。气缸两端有端盖,还有轴承座等。
3 贯穿叶片式气动马达工作原理
当压缩气体自图1的进气孔4进入转子外表面、气缸内表面、两叶片之间的气腔(也称基元容积)时,驱动叶片并带动转子一起作逆时针旋转,从输出轴输出功率及转矩。
由于进气过程中转子旋转,气腔容积逐渐增大,当气腔容积达到一定容积V1时,该气腔与进气孔口4切断,随后转子继续转动,容积由V1不断增大到最大容积V2,与排气孔口5接通进行排气。因此压缩气体在气腔内由进气过程、膨胀过程、排气过程三者组成一个理论循环过程。这个理论循环过程由图2表示。
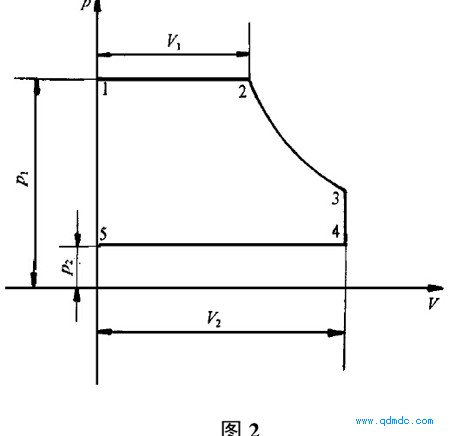
图2中1-2为进气过程,2-3为绝热膨胀过程, 4-5为排气过程。在绝对压力为p、容积为V的p-V图中,面积1-2-3-4-5表示一理论绝热过程中,压缩气体对气动马达所作的绝热理论功,按文献〔2〕可表示如下:
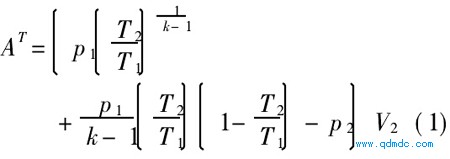
式中 AT一理论绝热过程中压缩气体对气动马达所作的绝热理论功, J
p1--进气绝对压力, Pa
T1--进气绝对温度, K
p2--排气绝对压力, Pa
T2--排气绝对温度, K
V2--排气容积, m3
k--气动马达的工作介质的绝热指数,采用压缩空气时k=114
AT还可表示为:
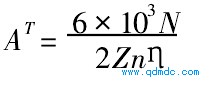
式中 N--马达输出功率, kW
n--气动马达的额定转速, rPmin
Z--贯穿叶片的数目
G--气动马达绝热总效率,G=0.42~0.5
通常Z=2,也可以Z=1,本文中采用Z=2。
由式(2)计算出AT之后,p1、p2、T1、T2、
k为已知时,则由式(1)可计算出V2:
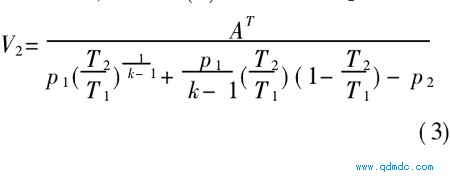
图2中的2)3之间为绝热膨胀,则V1与V2之间有下列关系式:
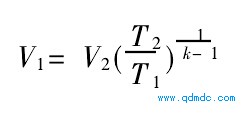
4 气缸内壁的型线方程
图3中每个叶片的径向长度为2R。当叶片处于水平位置时,这个叶片的中点是气
缸内壁型线的中心,有:
e=R-r
式中 e--偏心距, m
R--气缸内壁型线的创成半径, m
r)--转子半径, m
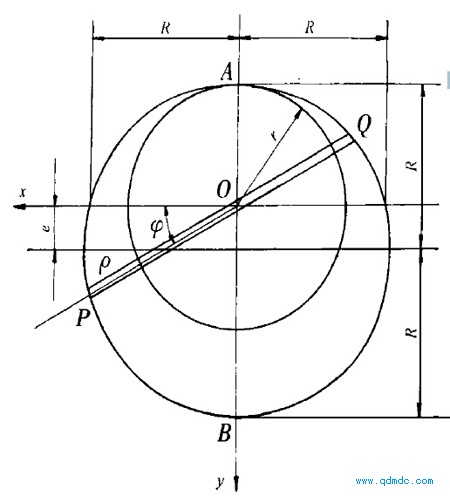
图3
以图3中的O点为参考点,气缸内壁的长半径OB为:
OB=e+R=e+(r+e)=r+2e
气缸内壁的短半径OA为:
OA=r
图3中,O为极点,Ox轴为极轴,叶片与Ox轴重合位置起,U=0,逆时针方向U为正,矢径Q对应的角为U。由于是贯穿叶片,无论叶片处于任何位置,叶片这一端的极径增加,则另一端的极径减小,一个叶片在一条直线上的两极径之和保持为2R,即
OP+OQ=2R
根据这个特点,理论上气缸内壁的型线为帕斯卡涡线,图3所示的极坐标系中,该涡线的方程式为:
Q=R+esinU
5 气腔面积计算
从图4中两相邻叶片oa及od之间的气
腔面积a-b-c-d中取微小面积,该微元的极
角为A,极径为Q,微元的面积为
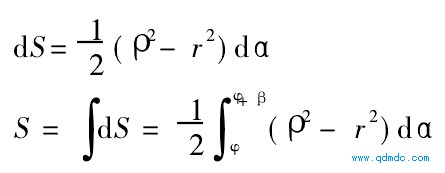
将气缸内壁型线的方程代入,得

式中 B--两相邻叶片之间的夹角,rad 本文中两个贯穿叶片互相垂直,有

将式(11)代入式(10),得
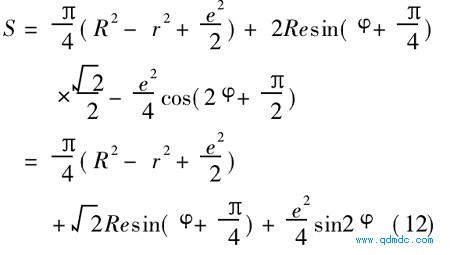

因叶片有厚度,实际上最大气腔面积将小于计算值Smax。由于叶片厚度的影响使气腔面积减小的程度,可用一个系数K来近似计算:
S1=KSmax
或者 S1=K〔P4(R2-r2+e22)+ 2Re+e24〕
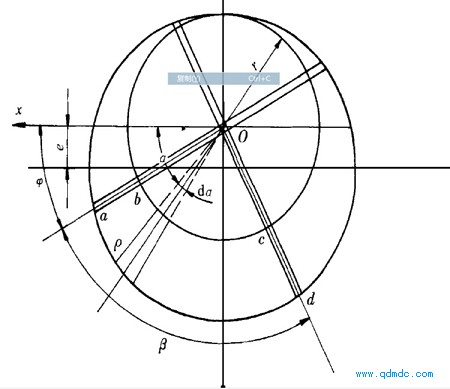
式中 S1--考虑叶片厚度的影响后气腔的面积,m2
K--影响系数
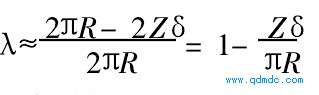
前面已经约定Z=2,式(16)变为

6 气腔容积计算
气腔容积为:
V=B
式中 V--气腔容积, m3
B--气腔轴向宽度, m
最大气腔容积为
Vmax=V2=S1B
式中 Vmax--最大气腔容积, m3
由式(3)、式(19),得出叶片的轴向宽度
B=V2/S1
图1中,叶片旋转过程中切断进气孔口
4的位置角度U1确定如下。进气容积V1由式(4)得出,由式(12)算出面积S,
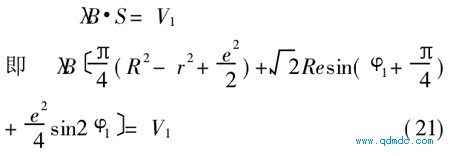
由式(21)可解出U1。
7 主要几何参数计算
(1)气腔轴向长度或贯穿叶片轴向宽度B按式(20)决定。
(2)创成半径及偏心距确定图3中创成半径R与偏心距e的比值K
称为气缸内壁型线的形状参数,即
K=Re
根据文献〔1〕的研究表明,在下述范围内选择K值比较适宜:
K=4~10
偏心距e按下列范围选取:
e=01005~0101
当K、e选取之后,R随之确定:
R=Ke
(3)贯穿叶片几何尺寸计算
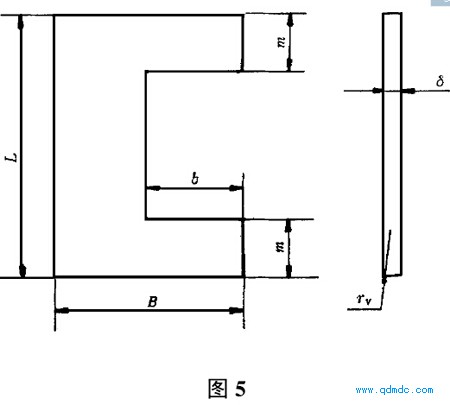
图5中
L=2R
式中 L--叶片径向长度, m叶片厚度可先选定,最后进行弯曲强度校核,计算叶片弯曲强度的方法可参阅文献
〔3〕。
D=0.1004~0.1006
式中 D--叶片厚度, m
图5中的贯穿叶片缺口轴向宽度b略小于BP2。
m的长度为
m=215e
叶片顶端圆角半径为:
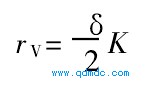
式中 rV--叶片顶端圆角半径, m
(4)转子外半径计算
r=R-e
式中 r--转子外半径, m
(5)马达进、排气孔口位置的确定
图1中,进气孔位置U1由式(21)确定。排气孔口位置U2=P4+P2=3P4。
按文献〔2〕,U3、U4为:
U3=U4=Dr
8 进、排气接管内直径计算
进、排气接管分别与进、排气孔口连接(进、排气接管在图1中未表示出来)。进气接管内气流平均速度v1通常为20~25mPs,进气接管内直径d1的计算方法如下:
每秒钟流过进气接管断面Pd214的压缩气体容积流量为Pd21v14,应与每秒钟进入气腔的容积流量4V1n60相等,即:
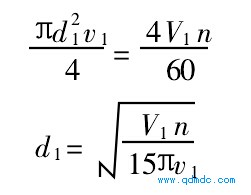
式中 d1--进气接管内直径, m
v1--进气接管内气流平均速度, mPs排气接管内直径与进气接管内直径相等。
通常排气接管内气流平均速度比v1大很多。
9 气动马达耗气量计算
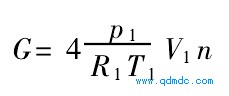
式中 G--气动马达每分钟耗气量,kgPmin
R1--压缩气体常数。对于压缩空
气,R1=287114 JP(kg.K)
10 结束语
贯穿叶片式气动马达是一种新型的马达,它的最大特点是采用贯穿式叶片,从而提高了气动马达叶片使用寿命。该种马达气缸内壁型线不是圆周曲线而是帕斯卡涡线。它具有一切叶片式气动马达的优点。



