活塞式气动马达力学模型及性能分析

　气动马达从起动到转速稳定下来后, 在任一时刻排气量都等于进气量, 表示为, q 排=q 进。由此利用能量守恒原理, 定量研究发动机稳态时, 阻力矩和转速的关系。

　　显然, 四个活塞缸是按一定顺序依次对曲轴发生作用, 四个活塞缸对曲轴旋转的“贡献”是一致的, 要研究发动机整体, 可以先研究单个活塞对曲轴的作用原理。如图2 所示, 把典型的“曲柄连杆机构”, 作为研究单个活塞对曲轴作用的力学模型。

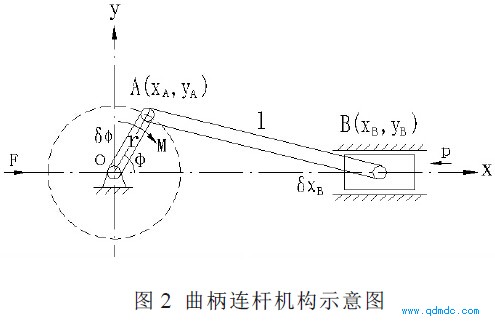
　　旋转半径r 和曲轴偏心距一致, 连杆长度l 和滚圈半径一致, p 为活塞对滚圈的压力, F 表示排气过程对旋转的阻力, M表示旋转负荷即阻力矩。取曲柄的转角! 为广义坐标, 则滑块B 的坐标xB 可用广义坐标! 表示如下:

　　χB=rcosφ+√l2- r2sin2φ

　　而广义虚位移δφ与滑块B 相应产生的虚位移δχB 之间的关系可由上式变分求得, 即

　　令:

　　根据式( 1) 有

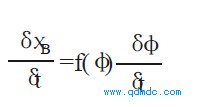
　　也可表示为v=f(φ)ω,式中v 为活塞的推动速度, ω为曲轴的角速度。我们知道, 活塞虚位移产生的主动元功W主

　　W主=pq=psv

　　式中, s 为活塞的截面积, v 为活塞速度, p 为气动马达的给定气压, q 为排气量。

　　曲轴转动形成的约束元功W转为

　　W转=Mω

　　式中, M为曲轴的阻力矩( 负荷)气缸排气形成的约束元功W排为

　　W排= Δpq

　　式中, Δp 表示气缸排气需要的压力, 在排气口结构大小确定以后, 与排气量的平方成正比, 即, Δp=Kq2 于是有, W排=Kq3=K( ps) 3。K 是表征排气口结构大小的常数。

　　根据功能平衡原理(忽略所有构件的重量、摩擦力和泄漏):

　　W主=W转+W排

　　于是, psv=Mω+K( sv) 3

　　psf( φ) ω=Mω+Ks3f3( φ) ω3

　　因为总有ω>0 , 所以有

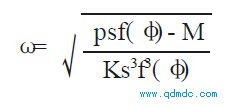
　　( 3)

　　分析式( 3) 知道, 角速度ω随着φ变化, 发动机在不同位置有不同的速度, 同时, 因为总有ω>0,因此有psf( φ) - M>0, 满足这一关系的是一个开区间, 设为( α, β) , 并称( α, β) 为有效作用区间, 这里会出现两种情况: ( 1) β- α>π/2; ( 2) β- α<π/2。

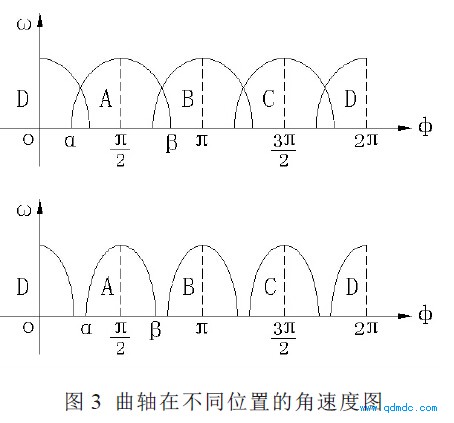
　　图3表达了两种情况下, 曲轴在不同位置的角速度。这里需要特别指出的是, 当β- α>π/2 时, 会有两个气缸同时对曲轴旋转起作用, 发动机的配气阀在这时增加一个排气口。设第一个气缸的排气量为q1, 第二个为q2, 如果只有一个出口, W 排=K( q1+q2) 3>>Kq13+Kq23, 但增加一个排气口后, 基本能实现,W排=W1+W2, 从而能各自使用公式( 3) 分别计算出ω1、ω2, 这时曲轴的总的角速度ω=ω1+ω2。再看β-α<π/2 的情况要简单一些。我们很容易推断出, 不管哪种情况, 发动机的平均角速度计算公式为:

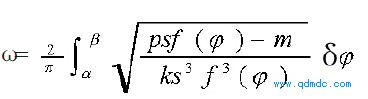
　　( 4)

　　发动机转速n 为

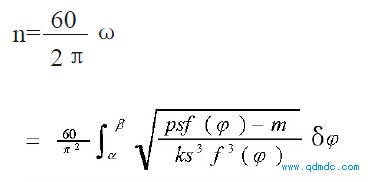
　　( 5)

　　式( 5) 即是活塞发动机转速的计算公式, 从公式( 5) 知, 在发动机结构确定、气压给定以后, 计算在一定负荷下发动机的转速, 首先要利用关系psf(φ)- m>0, 求取初始角α和终了角β然后根据公式( 5) 计算出转速n。